电子凸轮——五次多项式计算

五次多项式是常用的轨迹规划算法。由于其数学特性，可保证一阶和二阶导数连续，能够实现从起点到终点的位置、速度、加速度三重平滑过渡，避免突跳带来的机械冲击，提高系统稳定性与寿命，所以常用于凸轮设计、机器人路径规划、数据拟合等场景中。

五次多项式公式

位置函数

$P(x) = k_5x^5 + k_4x^4 + k_3x^3 + k_2x^2 + k_1x + k_0 \\$

速度函数（一阶导数）

$V(x) = 5k_5x^4 + 4k_4x^3 + 3k_3x^2 + 2k_2x + k_1 \\$

加速度函数（二阶导数）

$A(x) = 20k_5x^3 + 12k_4x^2 + 6k_3x + 2k_2 \\$

给定的起始和结束的主轴位置 x、从轴位置 y、速度 v、加速度 a 所构造的约束方程。

$\begin{aligned} P(x_0) = y_0 \\ V(x_0) = v_0 \\ A(x_0) = a_0 \\ P(x_1) = y_1 \\ V(x_1) = v_1 \\ A(x_1) = a_1 \end{aligned} \\$

系数k0~k5通用解

根据给定的起始和结束的主轴位置、从轴位置、速度、加速度以及主轴相对位移（ Δx ），可以得到如下解：

$\begin{aligned} \Delta x &= x_1 - x_0 \\ \Delta y &= y_1 - y_0 \\ k_0 &= y_0 \\ k_1 &= v_0 \\ k_2 &= \frac{a_0}{2} \\ k_3 &= \frac{1}{2\Delta x^3} \left[ 20\Delta y - (8v_1 + 12v_0)\Delta x - (3a_0 - a_1)\Delta x^2 \right] \\ k_4 &= \frac{1}{2\Delta x^4} \left[ -30\Delta y + (14v_1 + 16v_0)\Delta x + (3a_0 - 2a_1)\Delta x^2 \right] \\ k_5 &= \frac{1}{2\Delta x^5} \left[ 12\Delta y - 6(v_1 + v_0)\Delta x + (a_1 - a_0)\Delta x^2 \right] \end{aligned} \\$

代入数据计算

电子凸轮——五次多项式计算 PLC控制器第6张
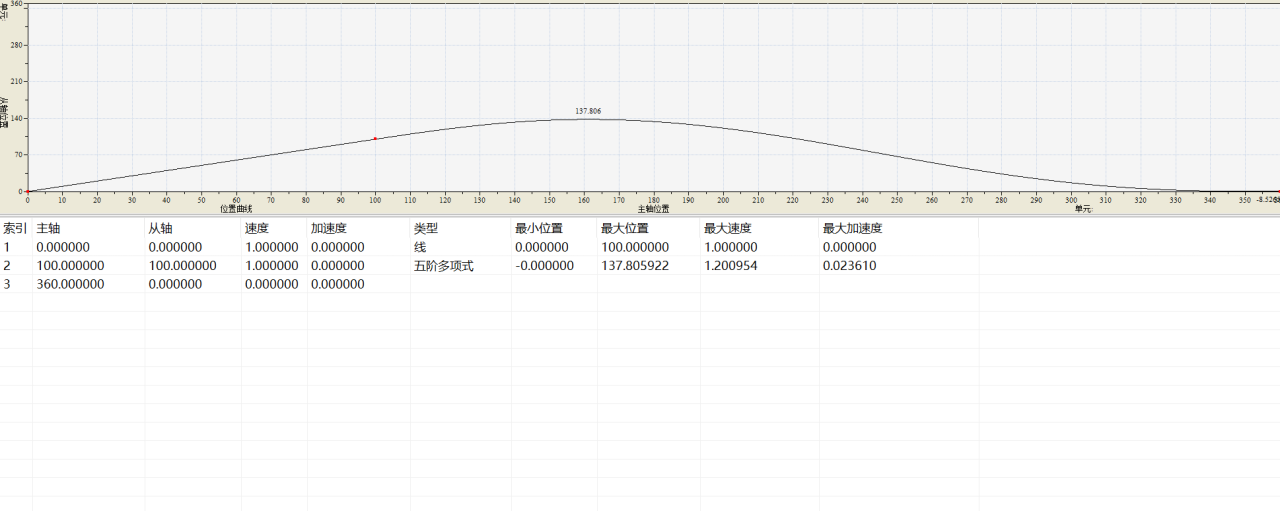
已知凸轮点数据

（x0，y0，v0，a0） = （100，100，1，0）

（x1，y1，v1，a1） = （360，0，0，0）

结合上方公式，求得：

$\begin{aligned} k_0 &= 100\\ k_1 &= 1\\ k_2 &= 0\\ k_3 &= -0.000145653\\ k_4 &= 0.000000783411\\ k_5 &= -0.00000000116148 \end{aligned} \\$

所以：

位置函数

$P(x) = -0.00000000116148 x^5 + 0.000000783411 x^4 - 0.000145653 x^3 + 1 x + 100 \\$

速度函数

$V(x) = -0.0000000058074 x^4 + 0.000003133644 x^3 - 0.000436959 x^2 + 1 \\$

加速度函数

$A(x) = -0.0000000232296 x^3 + 0.000009400932 x^2 - 0.000873918 x \\$

最大值求解

求位置函数的最大值，其实就是速度函数 V(x) = 0 时 [0, 260] 区间内所有方程的实根。

但是速度函数是一元四次方程，要去求它的根？？？

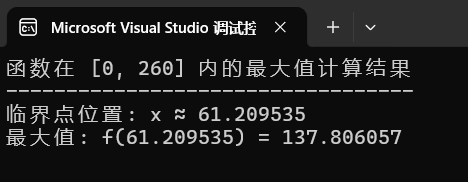
我并不清楚在数学上如何求解，所以只能通过程序，采用二分法尽量去逼近 f'(x) = 0 时，x 的值。

最后得到当 x ≈ 61.209535 时，最大值 V(61.209535) = 137.806057

电子凸轮——五次多项式计算 PLC控制器第11张

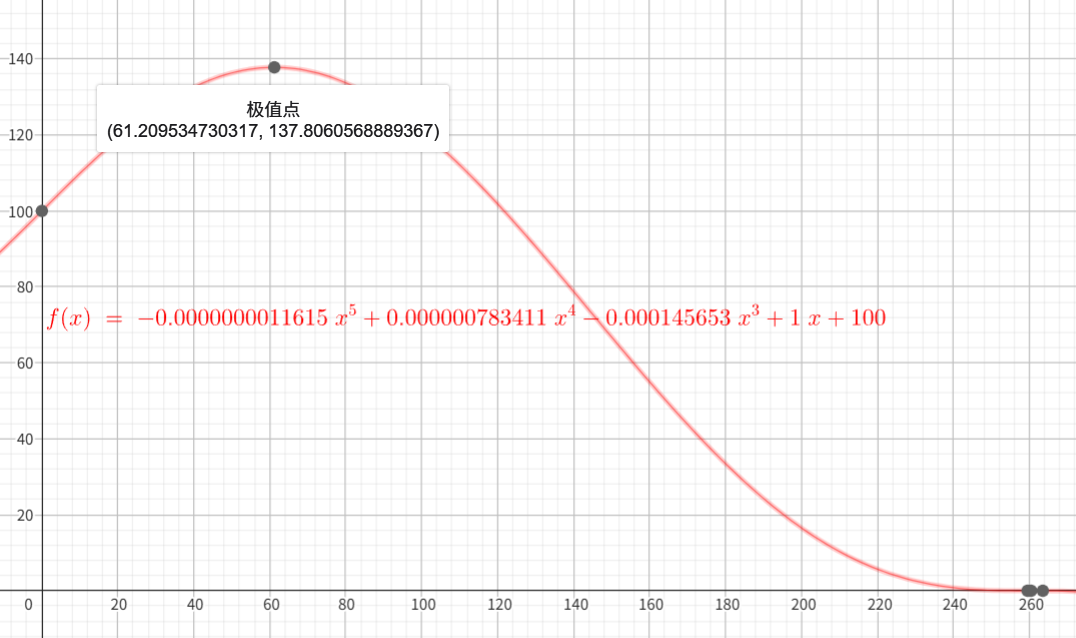
最后，通过GeoGebra 画出位置函数验证一下极值，确实符合计算结果。

电子凸轮——五次多项式计算 PLC控制器第12张

本文地址：https://www.52plc.cn/2026/01/industry/plc/cam.html
版权声明：欢迎分享本文，转载请保留出处！

发表评论 取消回复

发表评论取消回复